菱形作为一种特殊的四边形，在数学几何学中占有重要地位，菱形存在性专题研究旨在探讨菱形在不同条件下的存在性及其性质，本文将围绕这一主题展开，通过深入分析、研究菱形的基本性质、判定方法以及存在性证明，进一步拓展我们对菱形存在性的理解。

菱形的基本性质

菱形作为一种对称图形，具有许多独特的性质，菱形的四条边都相等，对角线垂直平分且相互平分对方，菱形具有中心对称性，即任意一点关于中心点对称，菱形的内角互补，即相邻两角之和为180度，这些性质为我们研究菱形存在性提供了基础。

菱形的判定方法

在实际问题中，我们需要根据给定的条件判断某个四边形是否为菱形，常见的判定方法包括：四边相等的四边形是菱形、对角线垂直的平行四边形是菱形以及对角线相互平分的四边形是菱形等，通过对这些判定方法的应用，我们可以判断特定条件下是否存在菱形。

菱形存在性证明

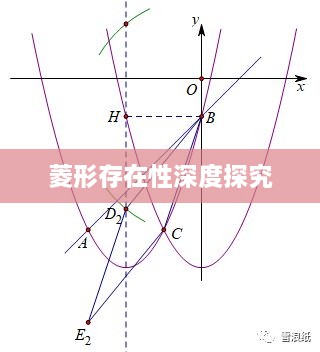
在证明某个图形是否为菱形时，我们需要根据具体的条件和已知的数学定理进行推导，在三角形中，如果两边相等且这两边所对的角相等，那么可以判定这个三角形为等腰三角形，进而推断出存在以这两边为边长的菱形，我们还可以利用平行四边形的性质，如对角线互相平分等，来证明菱形的存在性。

菱形存在性的应用

菱形存在性专题研究在实际应用中具有广泛的价值，在几何学中，菱形的研究有助于我们深入理解对称图形的性质，在图形设计、建筑美学等领域，菱形的存在性及其性质也得到了广泛应用，在解决实际问题时，如判断某个图案是否为菱形，或者利用菱形的性质进行图形构造等，都需要我们掌握菱形存在性的知识。

不同条件下的菱形存在性探讨

在实际问题中，我们可能会遇到各种不同类型的四边形，需要根据具体的条件判断是否存在菱形，在一个给定的多边形中，如果其边长满足菱形的定义（四边相等），则可以判断该多边形中存在菱形，在某些动态变化的图形中，如弹性碰撞过程中的物体运动轨迹可能形成菱形，我们需要根据物体的运动规律来判断菱形的存在性。

菱形存在性专题研究对于深入理解菱形的性质、判定方法以及存在性证明具有重要意义，通过深入研究这一主题，我们可以更好地应用菱形存在性的知识解决实际问题，如判断某个图案是否为菱形、利用菱形的性质进行图形构造等，希望本文能为读者提供关于菱形存在性专题的全面了解，并激发大家对几何学的学习兴趣。

建议与展望

为了更好地研究和理解菱形存在性专题，我们建议读者从以下几个方面进行深入学习：1）熟练掌握菱形的基本性质和判定方法；2）学习如何利用已知条件判断某个图形是否为菱形；3）在实际问题中尝试应用菱形存在性的知识；4）关注与菱形存在性相关的最新研究进展，如动态系统中的菱形存在性问题等，展望未来，我们希望菱形存在性研究能在更多领域得到应用，为数学几何学的发展做出更大的贡献。